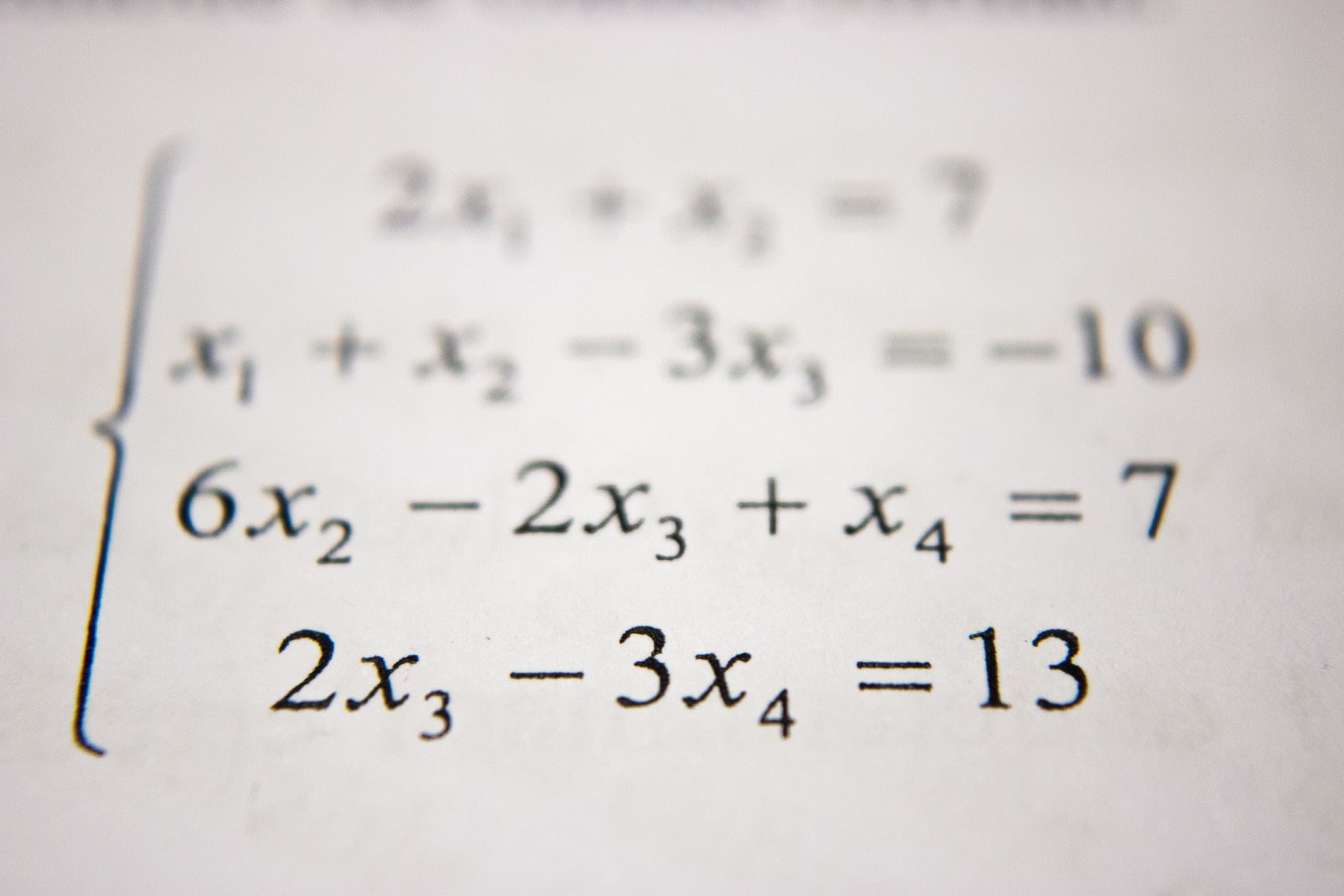Nắm vững các kiến thức toán học đằng sau những giải thuật về machine learning là một điều cực kỳ lợi hại. Hầu hết các kiến thức về machine learning đều ẩn chứa đằng sau các kiến thức về toán học cao cấp. Chẳng hạn như phương pháp stochastic gradient descent (viết tắt là SGD, Gradient Descent là thuật toán tối ưu hóa, trong đó Gradient là độ nghiêng của đường dốc, Decent là viết tắt của descending tức là giảm dần) khá khó hiểu vì được xây dựng dựa trên các lý thuyết về giải tích đa biến (multivariable calculus) và xác suất (probability).
Với những ai có kiến thức nền tảng vững chắc thì có thể nhìn nhận các ý tưởng một cách tự nhiên. Nếu bạn là người mới bắt đầu và không có các kiến thức toán học cao cấp thì việc tạo ra một lộ trình là thật sự khó. Bài viết này đưa ra cho bạn một lộ trình để có thể bắt đầu từ số 0 cho đến khi hiểu sau về cách thức hoạt động của các mạng nơ-ron hay còn gọi là mạng thần kinh (neural networks).
Tuy nhiên để cho đơn giản, chúng ta sẽ không cố gắng tìm hiểu tất cả mọi thứ trong một bài viết. Thay vào đó, bài viết tập trung vào vào việc định hướng và như vậy bạn có thể học hỏi các chủ đề khác nhau một cách dễ dàng.
Thay vì đọc bài này một lần rồi thôi, bạn nên sử dụng nó như một bảng tham khảo trong suốt quá trình học của mình. Đây có lẽ là cách tốt nhất để học: bạn có được lộ trình, và việc còn lại là phải thực sự học hỏi chăm chỉ.
Các nền tảng
Machine learning được xây dựng dựa trên ba kiến thức toán học chính: đại số tuyến tính (linear algebra), giải tích (Calculus) và lý thuyết Xác suất (probability). Và vì lý thuyết xác suất được xây dựng trên nền tảng Giải Tích và đại số tuyến tính nên chúng ta sẽ bắt đầu với hai môn này trước. Bạn có thể học Giải tích và Đại số tuyến tính một cách độc lập và đó là các kiến thức cốt lõi.
Giải tích
Giải tích là môn nghiên cứu về các phép tính vi phân (differentiation) và tích phân (integration). Về cơ bản, một mạng neuron (neural network) là một phép tính khả vi (differentiable function). Và như vậy, giải tích là công cụ nền tảng để huấn luyện mạng nơron như chúng ta sẽ thấy dưới đây.
Để có thể làm quen với các khái niệm, bạn cần phải làm cho mọi thứ thật sự đơn giản và chỉ nghiên cứu các hàm với biến đơn khi bắt đầu. Theo định nghĩa, đạo hàm của một hàm số được xác định như sau:

Trong đó tỉ lệ h cho trước là độ dốc của đường thẳng giữa các điểm (x, f(x)) và (x+h, f(x+h)).
Trong giới hạn (limit), đây là hệ số gốc của tiếp tuyến tại điễm x. Đồ thị dưới đây cho thấy điều đó
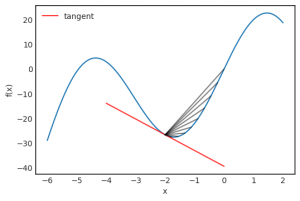
Vi phân có thể dùng để tối ưu hóa các hàm số: đạo hàm là 0 tại điểm cực đại địa phương (local maxima) hoặc cực tiểu địa phương (local minima) (Tuy nhiên điều này lại không đúng theo hướng ngược lại, xem f(x) = x³ tại 0). Các điểm nơi có đao hàm là 0 được gọi là các Điểm Tới Hạn hay còn gọi là Điểm Cực Trị (critical points). Cho dù một điểm tới hạn là cực đại hay cực tiểu nó có thể được xác định bằng cách xem tại đạo hàm bậc 2 (second derivative):

Có một số quy luật căn bản về vi phân nhưng quan trọng nhất là quy tắc dây chuyền hay còn gọi là quy tắc hàm của hàm (chain rule)
![]()
Quy tắc này cho chúng ta biết cách tính đạo hàm của các hàm hợp (composed function)
Tích phân (Integration) thường được gọi là sự đảo ngược của vi phân (differentiation). Điều này hoàn toàn đúng vì:

Trong đó chứa bất kỳ hàm khả tích (integrable function) f(x) nào. Tích phân (integral) của một hàm có thể xem như khu vực xác định (signed area) dưới đường cong. Ví dụ:

Vì khi hàm có giá trị âm, khu vực này cũng có giá trị âm.
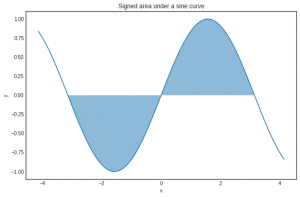
Tích phân giữ vai trò chính trong khái niệm giá trị mong đợi (expected value). Ví dụ, số lượng lớn các ngẫu nhiên (quantities like entropy) hay phân kỳ Kullback-Leibler (Kullback-Leibler divergence) được xác định dưới dạng các tích phân.
Linear algebra – Đại số tuyến tính
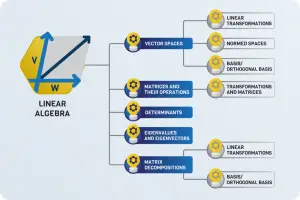
Như đã đề cập bên trên, các mạng thần kinh là một chuỗi các phép tính được huấn luyện sử dụng các công cụ của giải tích. Tuy nhiên, chúng lại được mô tả dùng các khái niệm về đại số tuyến tính như nhân ma trận.
Đại số tuyến tính – linear algebra – là một chủ đề rất rộng có liên quan tới rất nhiều khía cạnh của lĩnh vực machine learning. Vì vậy phần này rất quan trọng.
Không gian Vector (Vector spaces)
Để có thể hiểu được tốt về đại số tuyến tính, chúng ta hãy bắt đầu với các không gian vector. Tốt hơn hết là hãy xem xét về một trường hợp đặc biệt. Bạn có thể xem mỗi điểm trên một mặt phẳng là một bộ dữ liệu (tuple)
![]()
Trong đó có các vectors hướng từ 0 đến điểm (x₁, x₂). Bạn cũng có thể cộng các vectors với nhau và nhân chúng với các đại lượng vô hướng (scalar):
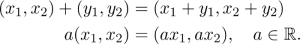
Đây là mô hình nguyên mẫu của một không gian vector. Một cách tổng quát, một tập các vector V là một không gian vector trên các số thực nếu bạn có thể cộng các vector với nhau và nhân các vector với một số thực như các thuộc tính dưới đây:
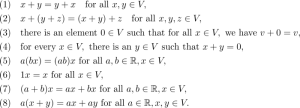
Đọc đến đây có lẽ bạn hơi hoảng hốt. Tất cả mọi thứ bạn xem cho đến lúc này thật đáng sợ. Nhưng thật ra nó không như vậy. Những công thức trên chỉ nhằm chỉ ra rằng các vector có thể cộng với nhau và nhân với nhau. Khi nghĩ về các không gian vector, nó sẽ có ích nếu bạn tư duy các mô hình kiểu như sau:
![]()
Không gian định chuẩn – Normed spaces
Nếu bạn thấy mình đã hiểu rõ về không gian vector, bước tiếp theo sẽ là tìm hiểu cách đo lường chiều dài (magnitude) của các vector. Mặc định các không gian vector chính nó không cung cấp công cụ nào để chúng ta có thể làm điều đó. Vậy làm thế nào trên một mặt phẳng? Chúng ta có:
![]()
Đây là một trường hợp đặc biệt của một chuẩn norm. Một cách tổng quát, một không gian vector V là được chuẩn hóa (normed) nếu có một hàm số:
![]()
Được gọi chuẩn norm khi:

Một lần nữa, điều này lại có thể khiến bạn lo lắng. Tuy nhiên đây là những khái niệm cơ bản và đơn giản. Có nhiều chuẩn norm nhưng quan trọng nhất là p-norm

(Với p = 2 chúng tra sẽ có trường hợp đặc biệt – norm 2.)
Một chuẩn khác cũng rất quan trọng là supremum norm (hay có thể gọi là uniform norm)
![]()
Đôi lúc, cũng giống như trường hợp p = 2, norm hình thành từ inner product (phép nhân vô hướng của 2 vector), là một chức năng song tuyến tính (bilinear function):
![]()
Như vậy:

Một không gian vector với một tích vô hướng (inner product) được gọi là không gian tích vô hướng (inner product space). Có thể thấy qua ví dụ về một Euclidean product cổ điển sau:
![]()
Mỗi inner product có thể đươc chuyển thành norm bằng phép tính:

Trong trường hợp tích vô hướng của 2 vector là 0, chúng ta gọi các vectors là trực giao (orthogonal) với nhau.
Cơ sở (Basis) và trực giao/trực chuẩn (orthogonal/orthonormal basis)
Mặc dù các không gian vector là vô hạn, ta có thể tìm thấy tập giới hạn các vectors có thể dụng để mô tả tất cả các vector trong một không gian. Ví dụ, trên một mặt phẳng ta có:
![]()
Trong đó:
s
Đây là một trường hợp đặc biệc của Cơ sở (basis) và trực chuẩn cơ sở (orthonormal basis).
Một cách tổng quát, Cơ sở (basis) là một tập hợp nhỏ nhất các vectors:
![]()
Việc kết hợp các tuyến tính mở rộng không gian vector

Một basis (cơ sở) luôn hiện hữu trong bất kỳ không gian vector nào. Không nghi ngờ gì, một Basis đơn giản hóa mọi thứ khi chúng ta đề cập đến không gian tuyến tính (linear spaces)
Khi các vectors trong một cơ sở trực giao với nhau, ta gọi đó là Cơ sở trực giao (orthogonal basis). Nếu các chuẩn trong vector cơ sở có chiều dài là 1 cho một Cơ sở trực giao, ta gọi đó là trực chuẩn (orthonormal)
Ánh xạ tuyến tính – Linear transformations
Một trong những chủ đề chính liên quan đến không gian vecor là các ánh xạ tuyến tính (linear transformations). Nếu bạn đã tìm hiểu về mạng neuron thì chắc hẳn bạn biết được là một trong những nền tảng tạo nên các blocks là các lớp:
![]()
Trong đó A là một ma trận, b và x là các vector và σ là hàm sigmoid hoặc bất kỳ hàm kích hoạt (activation function) nào. Ax chính là ánh xạ tuyến tính. Một cách tổng quát, một hàm
![]()
Là một ánh xạ tuyến tính giữa không gian vector V và W nếu:
![]()
Giữ cho tất cả x, y và V, và tất cả các số thực a.
Một ví dụ cụ thể đó là sự xoay quang điểm gốc trong mặt phẳng là biến đổi hay ánh xạ tuyến tính
Không có gì nghi ngờ về một thực tế quan trọng về ánh xạ tuyến tính là chúng có thể được sử dụng trong các ma trận và bạn sẽ tìm hiểu trong các phần dưới đây.
Ma trận và các toán tử về ma trận (Matrices and their operations)
Nếu bạn đã nắm vững về ánh xạ tuyến tính, bạn có thể chuyển học nghiên cứu về ma trận. Thông thường trong các khóa học người ta sẽ dạy cho bạn về ma trận trước. Tuy nhiên chúng ta có lý do để học sau phần ánh xạ tuyến tính và bạn sẽ thấy dưới đây.
Một trong những toán tử quan trọng trong các ma trận là các matrix product. Một cách tổng quát nếu A và B là các ma trận được định nghĩa bởi:
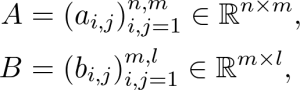
Khi đó:

Bạn có thể thấy có vẻ khó hiểu nhưng thực sự không quá phức tạp như bạn nghĩ. Hãy xem ví dụ dưới đây cho thấy cách tính phần tử trong hàng thứ 2, cột thứ nhất của ma trận.
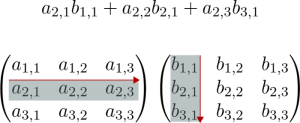
Lý do tại sao nhân ma trận (matrix multiplication) được thực hiện theo cách đó vì các ma trận thể hiện các ánh xạ tuyến tính giữa các không gian vectors. Nhân ma trận là thành phần của ánh xạ tuyến tính.
Định thức – Determinants
Khó có thể phản bác, là định thức (determinant) là một trong những khái niệm khó nhằn nhất trong đại số tuyến tính. Định thức được xác định hoặc là bằng một định nghĩa đệ quy (recursive definition) hoặc là một tổng mà lặp qua tất cả các hoán vị (permutations). Dù xác định bằng cách nào đi nữa thì cũng rất khó để vận dụng nếu bạn không có kinh nghiệm đáng kể trong trong toán học.
Bạn có thể xem thêm về định thức trong một video rất hay dưới đây:
Tóm lại, định thức của một ma trận diễn tả làm thế nào thể tích của một vật thể thay đổi theo phép ánh xạ tuyến tính tương ứng. Nếu sự chuyển đổi (transformation) thay đổi các định hướng thì dấu của định thức là âm
Giá trị riêng (eigenvalues), Vector riêng (eigenvectors) , và ma trận phân rã (matrix decompositions)
Một khóa học về đại số tuyến tính thường kết thúc với các chủ đề về giá trị riêng (eigenvalues)/vector riêng (eigenvectors) và một số ma trận phân rã (matrix decompositions), tức phân tích một ma trận ra thành tích của nhiều ma trận đặc biệt khác, ví dụ như phương pháp Singular Value Decomposition
Giả sử chúng ta có một ma trận A. Số λ là một giá trị riêng của A nếu có một vector x (gọi là vector riêng) như sau:
![]()
Nói một cách khác, ánh xạ tuyến tính được thể hiện bởi A là một một tỉ lệ của λ đối với vector x. Khái niệm này đóng một vai trò quan trọng trong đại số tuyến tính (và cả các lĩnh vực trong thực tế ứng dụng đại số tuyến tính một cách rộng rãi)
Tới thời điểm này, bạn đã sẵn sàng để làm quen với vài cách thức phân rã ma trận. Vậy các ma trận nào là tốt nhất cho việc tính toán này? Câu trả lời là ma trận đường chéo (diagonal matrix). Nếu một phép ánh xạ tuyến tính có một ma trận đường chéo, thì việc tính giá trị của nó trên một vectơ tùy ý là rất nhỏ.

Hầu hết các dạng đặc biệt với mục đích phân rã một ma trận A thành một tích các ma trận (product of matrices), đều có ít nhất một ma trận là đường chéo. Phương pháp Singular Value Decomposition, hay ngắn gọn là SVD, là phương pháp thông dụng nhất, trong đó có các ma trận đặc biệt U, V và một ma trận đường chéo Σ sao cho
![]()
Trong đó U và V được gọi là ma trận unita (unitary matrices).
Phương pháp SVD cũng được dùng để thực hiện phép phân tích thành phần chính (Principal Component Analysis), một trong những phương pháp đơn giản nhất và được biết đến nhiều nhất trong việc giảm chiều dữ liệu (dimensionality reduction)
Giải tích đa biến – Multivariable calculus

Đây là phần mà trong đó đại số tuyến tính và giải tích kết hợp với nhau, tạo ra các nền tảng cho các công cụ dùng để huấn luyện các mạng neuron: thuật toán tối ưu hóa (gradient descent). Theo cách nói của toán học, một mạng thần kinh là một hàm có nhiều biến trong đó số biến số có thể đến hàng triệu.
Tương tự như phép tính đơn biến, hai chủ đề chính ở đây là phép tính vi phân và tích phân. Giả sử ta có hàm:
![]()
Ánh xạ các vectors ra các số thực. Với 2 chiều, tức n=2, bạn có thể hình dung ra được các plot như là một mặt phẳng. Vì con người không nhìn cao hơn ba chiều, rất khó để mường tượng ra các hàm có nhiều hơn 2 biến thực:
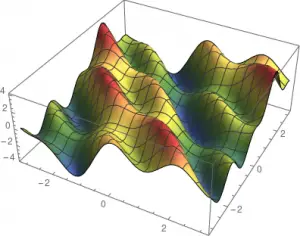
Phép tính vi phân nhiều biến – Differentiation in multiple variables
Trong phép tính một biến, đạo hàm là hệ số góc của đường tiếp tuyến. Làm sao để bạn xác định các tiếp tuyến? Một điểm trên một mặt phẳng có vài tiếp tuyến chứ không chỉ có một. Tuy nhiên có 2 tiếp tuyến đặc biệt: một song song với mặt phẳng x-z và một song song với mặt phẳng y-z. Hệ số góc của chúng được xác định bằng các đạo hàm riêng (partial derivatives) được xác định bởi:

Trong đó, bạn lấy đạo hàm của hàm số có được bằng cách lấy đạo hàm theo một biến và giả thuyết rằng các biến khác là hằng số.
Các tiếp tuyến theo các hướng đặc biệt này tạo thành mặt phẳng tiếp tuyến (tangent plane):
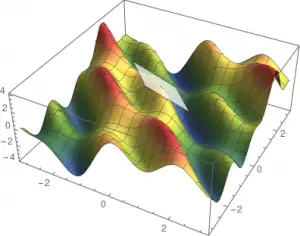
Độ dốc – The gradient
Có một hướng đặc biệt khác: gradient. Gradient là một vector và được xác định bởi:
![]()
Gradient luôn hướng về hướng tăng lớn nhất, là tỷ lệ độ nghiêng của đường dốc. Gradient descent là thuật toán tối ưu hóa lặp có các bước thực hiện như sau:
- Tính toán độ nghiêng của đường dốc tại điểm x₀, điểm hiện tại của bạn
- Đi từng bước nhỏ theo hướng của gradient để đến điểm x₁. Kích thước của bước gọi là tốc độ học (leanring rate)
- Quay lại bước 1 và lặp lại quy trình cho đến khi hội tụ
Dĩ nhiên là có những điểm chưa hoàn hảo trong giải thuật này và vì vậy, nó luôn được cải tiến trong nhiều năm qua. Thuật toán gradient descent hiện đại sử dụng nhiều thủ thuật như kích thước bước thích ứng (adaptive step size), momentum và nhiều phương pháp khác mà chúng ta không đề cập chi tiết ở đây.
Trong thực tế việc tính toán Gradient là không hề dễ dàng. Các hàm thường được mô tả bởi thành phần của các hàm khác, ví dụ như lớp tuyến tính quen thuộc:
![]()
Trong đó A là một ma trận, b và z là các vectorz và σ là hàm sigmoid. Tất nhiên, có thể có các hàm kích hoạt (activations) khác nhưng để cho đơn giản chúng ta chỉ tập trung vào signmoid. Vậy thì làm sao bạn có thể tính toán được độ dốc? Tới thời điểm này, cũng chưa có gì rõ ràng trong việc định nghĩa gradient cho các hàm vector-vector. Hãy lấy ví dụ hàm dưới đây:
![]()
Luôn có thể được viết dưới dạng hàm vector vô hướng (vector-scalar fuction)

Gradient của g là được định nghĩa bởi ma trận mà hàng thứ k là phần tử thứ k của gradient:

Ma trận như vậy được gọi là đạo hàm toàn phần của g (total derivative of g)
Trong ví dụ của chúng ta:
![]()
Mọi thứ trở nên phức tạp vì nó bao gồm 2 hàm:
![]()
và
![]()
Được xác định bằng cách áp dụng thành phần sigmoid đơn biến. Hàm l có thể phân rã thành m hàm ánh xạ từ không gian vector n chiều cho các số thực.

trong đó:

Nếu tính toán đạo hàm toàn phần bạn sẽ có:
![]()
Đây là quy tắc dây chuyền cho các hàm đa biến (chain rule for multivariate functions) về tính tổng quát đầy đủ của nó. Không có nó, khó có thể tính gradient của các mạng nơ-ron.
Đạo hàm cấp cao – Higher-order derivatives
Tương tự với các đạo hàm đơn biến, gradient và các đạo hàm đóng một vai trò trong việc xác định xem một điểm cho sẵn trong không gian là điểm cực tiểu hay cực đại (local minima or maxima) hay cả hai. Hãy xem một ví dụ cu thể, huấn luyện một mạng thần kinh là tương đương với việc tối ưu hàm mất mát (loss function) trên các dữ liệu huấn luyện (training data) của các tham số. Đó là việc tìm các cấu hình tham số tối ưu w để đạt được giá trị cực tiểu.

trong đó:
![]()
Cho một hàm vector vô hướng n biến, có n² đạo hàm cấp hai hình thành nên ma trận Hesse (Hessian matrix). (Ma trận Hesse là ma trận vuông của đạo hàm từng phần bậc hai của một hàm số, do đó nó sẽ biểu thị độ cong của một hàm số nhiều biến)

Trong đa biến, định thức Hesse đóng vai trò của đạo hàm cấm hai. Tương tự như vậy, nó có thể được sử dụng để chỉ ra điểm cực trị critical point là cực tiểu, cực đại hay là điểm yên ngựa (saddle point). Điểm yên ngựa là là bất cứ điểm nào mà tất cả gradient của một hàm bằng 0, nhưng đó không phải là một điểm cực tiểu hay giá trị nhỏ nhất.
Lý thuyết xác suất – Probability theory

Lý thuyết xác suất (Probability theory) là ngành toán học nghiên cứu về xác suất, là nền tảng của tất cả các lĩnh vực khoa học.
Đặt các định nghĩa chính xác sang một bên, hãy cùng suy ngẫm một chút về xác suất đại diện cho điều gì. Giả sử bạn tung một đồng xu, với 50% cơ hội (hoặc 0,5 xác suất) đồng xu có mặt hình là ngửa. Sau khi lặp lại thí nghiệm 10 lần thì thu được bao nhiêu hình là ngửa như vậy?
Nếu câu trả lời là 5, bạn đã sai. Xác suất mặt hình là 0,5 không đảm bảo rằng mỗi lần ném thứ hai đều là mặt hình. Thay vào đó, điều đó có nghĩa là nếu bạn lặp lại thí nghiệm n lần trong đó n là một số thực sự lớn, số mặt hình sẽ rất gần với n / 2.
Bên cạnh những vấn đề cơ bản trên, có một số vấn đề cần phải tìm hiểu mà hai trong số đó là Giá trị kỳ vọng (expected value) và Entropy.
Giá trị kỳ vọng – Expected value
Giả sự bạn chơi một trò chơi với bạn. Bạn tung một xúc xắc sáu mặt và nếu kết quả là 1 hoặc 2, bạn thắng được 300 đô la. Nếu không, bạn thua 200. Bạn được trung bình mỗi vòng là bao nhiêu nếu bạn chơi trò chơi này đủ lâu? Bạn có nên chơi này không?
Bạn thắng 100 đô với xác suất 1/3, bạn mất 200 với xác xuất 2/3. Đó là khi nếu X là một biến ngẫu nhiên đại diện cho kết quả ném xúc xắc thì:
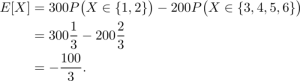
Đó là giá trị kỳ vọng, tức là số tiền trung bình bạn nhận được mỗi lần ném. Và vì giá trị nó là âm, bạn không nên chơi trò chơi này.
Một cách tổng quát, giá trị kỳ vọng được định nghĩa bởi công thức sau cho các biến ngẫu nhiên rời rạc (discrete random variables):
![]()
Và cho biến ngẫu nhiên giá trị thực (real-valued random variable), giá trị kỳ vọng được tính như sau:

Trong lĩnh vực machine learning, các hàm mất mát (loss functions) để huấn luyện mạng thần kinh là các giá trị kỳ vọng theo cách này hay cách khác.
Quy luật số lớn – Law of large numbers
Người ta thường sai lầm khi quy các hiện tượng về quy luật số lớn (law of large numbers). Ví dụ những người đánh bài đang thua lại có niềm tin rằng họ sẽ sớm thắng vì quy luật này. Điều này hoàn toàn sau. Hãy xem tại sao.
Giả sử các biến ngẫu nhiên sau đại diện cho các lần lặp lại độc lập của cùng một thí nghiệm. (như tung xúc xắc hoặc tung đồng xu):
![]()
Về cơ bản, luật số lớn sẽ được thể hiện trong biểu thức như sau:

Đó là giá trị trung bình của các kết quả trong dài hạn bằng với giá trị kỳ vọng.
Một cách giải thích dễ hình dung là nếu một sự kiện ngẫu nhiên được lặp lại đủ lần, các kết quả riêng lẻ có thể không quan trọng. Vì vậy, nếu bạn đang đánh bạc có giá trị kỳ vọng âm thì dù thỉnh thoảng bạn thắng, theo Quy luật số lớn bạn vẫn sẽ mất tiền.
Quy luật số lớn rất cần thiết trong phương pháp stochastic gradient descent đã đề cập ở phần đầu.
Lý thuyết thông tin – Information theory
Hãy cùng chơi một game. Tôi sẽ nghĩ ra một số có giá trị từ 1 đến 1024 và bạn hãy đoán nó. Bạn co thể đặt các câu hỏi, nhưng mục tiêu là càng ít câu hỏi càng tốt. Bạn cần bao nhiêu câu hỏi nào?
Nếu bạn chơi trò này một cách thông minh, bạn sẽ thực hiện một phép tìm kiếm nhị phân cho các câu hỏi của mình. Đầu tiên bạn có thể hỏi: số của anh là nằm trong số từ 1 đến 512? Khi có câu trả lời, bạn đã loại đi được một nửa. Với cách này bạn sẽ tìm ra được đáp án trong 10 câu hỏi:
![]()
Nhưng nếu bạn không sử dụng phân phối đồng nhất (uniform distribution) khi chọn một số. Ví dụ bạn có thể dùng phân phối Poisson (Poisson distribution).
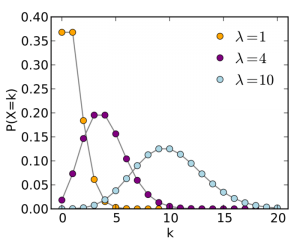
Bạn có thể sẽ cần ít câu hỏi hơn vì sự phân bố có xu hướng tập trung xung quanh các điểm cụ thể. (Điều này phụ thuộc vào tham số.)
Trong trường hợp đặc biệt khi sự phân phối tập trung vào 1 số suy nhất, bạn chẳng cần câu hỏi nào cũng đoán được chính xác kết quả. Nói chung, lượng câu hỏi phụ thuộc vào thông tin được phân phối. Sự phân phối đồng nhất (uniform distribution) chứa lượng thông tin ít nhất, trong khi singular distributrion (tạm dịch là phân phối kỳ dị) là thông tin nhất quán (pure information).
Entropy là một cách để định lượng và được định nghĩa bởi đẳng thức sau cho biến ngẫu nhiên rời rạc (discrete random variables):

Đối với các biến liên tục giá trị thực (continuous real-valued variable) ta có:

Nếu bạn đã từng làm việc với các mô hình phân lớp (classification models), bạn có thể đã gặp cross entropy loss, được định nghĩa bởi công thức:

Trong đó P là ground truth (tức là sự phân phối tập trung vào một lớp duy nhất) và P có mũ đại diện cho việc dự đoán của lớp. Công thức này dùng để đo lượng thông tin của các dự đoán so với ground truth. Khi các dự đoán khớp với nhau, cross-entropy loss là bằng 0.
Một đại lượng thường được dùng khác là phân kỳ Kullback-Leibler (Kullback-Leibler divergence), được xác định bởi:

Trong đó P & Q là hai phân phối xác suất. Về cơ bản đây là cross-entropy trừ đi entropy và có thể xem là định lượng sự khác nhau giữa hai phân phối. Nó rất hữu ích khi huấn luyện các generative adversarial networks (Tạm dịch: Mạng tạo đối kháng). Giảm thiểu phân kỳ Kullback-Leibler đảm bảo rằng hai phân phối là tương tự nhau.
Vượt ra khỏi nền tảng toán
Bài viết này đã cung cấp cho bạn lộ trình cần tìm hiểu về toán học để hiểu về các mạng nơ-ron và deep learning. Bạn có thể không cần giỏi toán để trở thành một lập trình viên giỏi nhưng để có thể làm tốt trong lĩnh vực Deep Learning hay Machine Learning, bạn cần có kiến thức toán học vững chắc. Bạn có thể xem bài gốc của tác giả Tivarda Danka tại đây. Ngoài ra, trong bài dịch còn có một số khái niệm và tham khảo từ Machine learning cơ bản và các nguồn khác. Nếu bạn thấy có những sai sót trong quá trình dịch thuật, hoặc góp ý, vui lòng để lại trong phần bình luận bên dưới.
Bạn có biết?
tham gia cộng đồng ITguru trên Linkedin, Facebook và các kênh mạng xã hội khác có thể giúp bạn nhanh chóng tìm được những chủ đề phát triển nghề nghiệp và cập nhật thông tin về việc làm IT mới nhất
Linkedin Page:
Facebook Group:
cơ hội việc làm IT : ITguru.vn