Top 14 câu hỏi phỏng vấn về lập trình của Apple

Làm việc tại Apple là một giấc mơ đối với nhiều developers, nhưng việc vượt qua được các cuộc phỏng vấn về lập trình không phải là một việc dễ dàng. Bài viết này tổng hợp 15 câu hỏi phỏng vấn hàng đầu về lập trình của Apple giúp bạn học hỏi và chuẩn bị tốt cho buổi phỏng vấn cho bất kỳ công ty công nghệ nào.

Câu hỏi  về Arrays và graphs

Q1: Determine sum of three integers

Mục tiêu của bài tập này là xác định xem tổng của ba số nguyên có bằng giá trị đã cho hay không.

Bài toán: Cho một mảng các số nguyên và một giá trị, hãy xác định xem có ba số nguyên nào trong mảng mà tổng của nó bằng giá trị đã cho hay không.

Hãy xem xét mảng này và tổng mục tiêu.

Hướng dẫn trả lời:

• Sắp xếp dữ liệu
• Lặp lại từ cả hai đầu

Xem toàn bộ giải pháp tại đây

Độ phức tạp:

• Runtime Complexity: Quadratic, O(n²)
• Memory Complexity: Constant, $O(1)$

Q2: Merge overlapping intervals

Mục tiêu của bài tập này là hợp nhất tất cả các khoảng (intervals) chồng chéo của một danh sách nhất định để tạo ra một danh sách chỉ có các khoảng loại trừ lẫn nhau. Đây là câu hỏi phỏng vấn lập trình có độ khó trung bình của Apple

Bài toán: Bạn có một mảng (danh sách) các cặp interval làm đầu vào trong đó mỗi khoảng có timestamp bắt đầu và kết thúc, được sắp xếp theo timestamp  bắt đầu. Hợp nhất các khoảng chồng chéo và trả về một mảng đầu ra mới. Để cho đơn giản,  các khoảng được biểu diễn dưới dạng các cặp số nguyên. 

Hãy xem xét một mảng đầu vào bên dưới. Các khoảng (1, 5), (3, 7), (4, 6), (6, 8) trùng nhau vì vậy chúng nên được hợp nhất thành một khoảng (1, 8). Tương tự, các khoảng (10, 12) và (12, 15) cũng chồng chéo và nên được hợp nhất thành (10, 15).

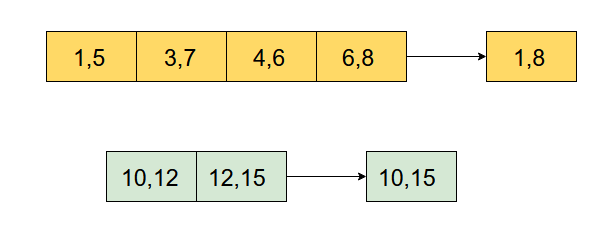
Hướng dẫn trả lời:

• Xem tại đây.
• Tìm hiểu thêm về overlapping interval tại đây

Độ phức tạp:

• Độ phức tạp về thời gian: Tuyến tính, O(n)
• Độ phức tạp về bộ nhớ: Tuyến tính, O(n)

Q3: Clone a Directed Graph

Mục tiêu của bài tập này là sao chép một biểu đồ có hướng (directed graph) và in ra biểu đồ được sao chép bằng cách sử dụng bảng băm và duyệt theo chiều sâu.

Bài toán: Cho nút gốc của một đồ thị có hướng, sao chép đồ thị bằng cách tạo một deep copy. Đồ thị được nhân bản sẽ có các đỉnh và các cạnh giống bảng gốc.

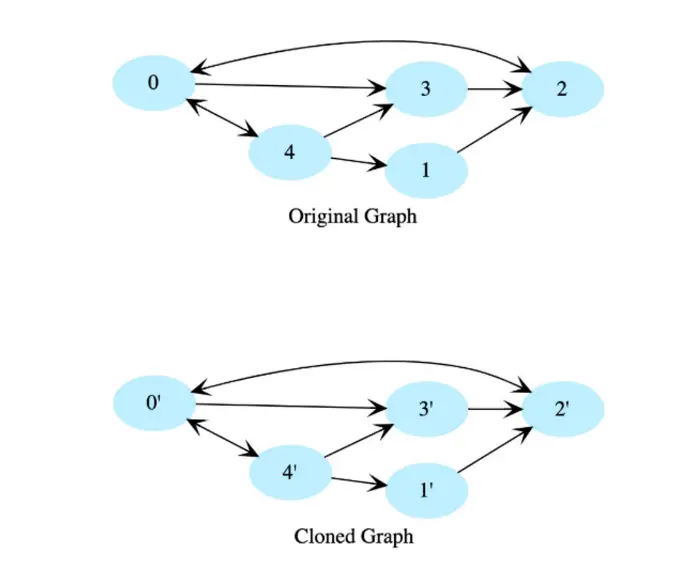
Hướng dẫn trả lời:

Sử dụng duyệt theo chiều sâu (depth first traversal)  và tạo một bản sao của mỗi node trong khi duyệt qua biểu đồ. Sử dụng bảng băm (hash table) để lưu trữ từng node đã hoàn thành, vì vậy chúng ta sẽ không truy cập lại các node tồn tại trong bảng băm đó. Khóa băm (hashtable key) sẽ là một node trong đồ thị gốc và giá trị của nó sẽ là node tương ứng trong đồ thị được sao chép.

Xem toàn bộ giải pháp và code mẫu

Độ phức tạp:

• Độ phức tạp về thời gian : Tuyến tính, O (n)
• Độ phức tạp của bộ nhớ: Logarit, O (n), trong đó n là số đỉnh trong đồ thị.

Câu hỏi phỏng vấn về danh sách liên kết

Q4: Add two integers

Mục tiêu của bài tập này là cộng hai số nguyên của hai danh sách liên kết.

Bài toán: Bạn được cung cấp các head pointer của hai danh sách liên kết trong đó mỗi danh sách liên kết đại diện cho một số nguyên (tức là mỗi node là một chữ số). Thêm chúng và trả lại danh sách liên kết mới.

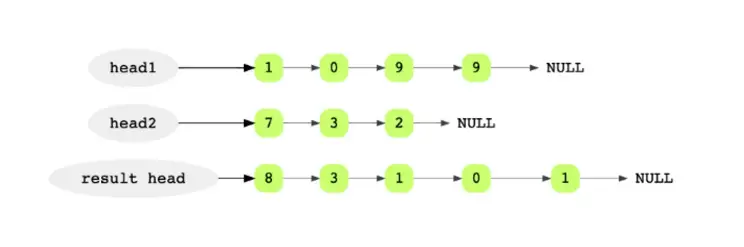
Hướng dẫn trả lời:

Để hiểu rõ hơn điều này, hãy xem xét một ví dụ. Giả sử chúng ta muốn thêm các số nguyên 9901 và 237. Kết quả của phép cộng này sẽ là 10138.

Các số nguyên được lưu trữ đảo ngược trong danh sách liên kết để thực hiện việc này dễ dàng hơn. Chữ số (digit) có nghĩa nhất của số là phần tử cuối cùng của danh sách liên kết. Để bắt đầu, chúng ta bắt đầu từ phần đầu của hai danh sách liên kết.

Ở mỗi lần lặp, chúng ta thêm các chữ số hiện tại của hai danh sách và chèn một node mới với digit kết quả ở đuôi của danh sách liên kết kết quả. Chúng ta cũng sẽ cần duy trì khả năng thực hiện cho từng bước.

Chúng ta thực hiệ điều này cho tất cả các chữ số trong cả hai danh sách liên kết. Nếu một trong các danh sách liên kết kết thúc sớm hơn (trong trường hợp này là 7-3-2), chúng ta sẽ tiếp tục với danh sách liên kết còn lại. Sau khi cả hai danh sách liên kết được thực hiện và không còn giá trị nào được thêm vào, thuật toán sẽ kết thúc.

Độ phức tạp:

• Độ phức tạp thời gian chạy: Tuyến tính, O (n)
• Độ phức tạp của bộ nhớ: Tuyến tính, O (n)

Q5: Merge two sorted linked lists

Mục tiêu của bài tập này là hợp nhất hai danh sách liên kết đã được sắp xếp. Câu hỏi này được xếp ở mức độ dễ trong phỏng vấn lập trình của Apple

Bài toán: Cho hai danh sách liên kết đã được sắp xếp, hãy hợp nhất chúng để danh sách liên kết thu được cũng được sắp xếp.

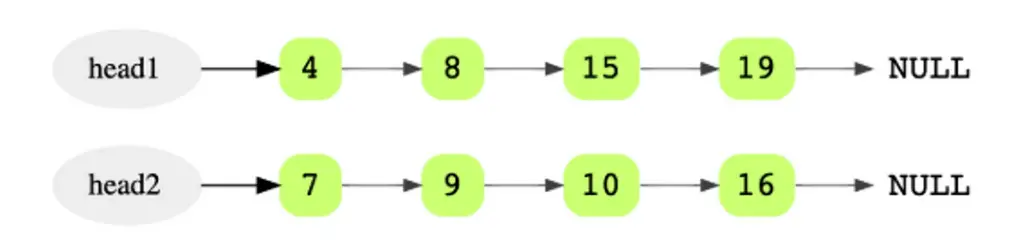
Kết quả:

Hướng dẫn trả lời:

Duy trì một con trỏ đầu (head pointer) và một con trỏ đuôi (tail pointer) trên danh sách liên kết đã hợp nhất. Chọn phần đầu của danh sách liên kết đã hợp nhất bằng cách so sánh node đầu tiên của cả hai danh sách được liên kết.

Đối với tất cả các node tiếp theo, hãy chọn node hiện tại nhỏ hơn và liên kết nó với phần đuôi của danh sách đã hợp nhất. Di chuyển con trỏ hiện tại của danh sách đó lên một bước.

Nếu vẫn còn một số phần tử trong chỉ một trong các danh sách, hãy liên kết danh sách còn lại này với phần cuối của danh sách đã hợp nhất. Ban đầu, danh sách liên kết được hợp nhất là NULL.

So sánh giá trị của hai node đầu tiên và làm cho node có giá trị nhỏ hơn trở thành node đầu của danh sách liên kết đã hợp nhất. Trong ví dụ này, nó là 4 từ head1. Vì đây là nút đầu tiên và duy nhất trong danh sách được hợp nhất nên nó sẽ là phần đuôi. Sau đó di chuyển head1 về phía trước một bước.

Xem toàn bộ giải pháp và code mẫu

Độ phức tạp:

• Độ phức tạp của thời gian chạy: Tuyến tính, O(m + n), trong đó m và n là độ dài của danh sách được liên kết của chúng tôi
• Độ phức tạp của bộ nhớ: Hằng số, O (1)

Các câu hỏi phỏng vấn về Trees

Q6: Determine if two binary trees are identical

Mục tiêu của bài tập này là so sánh hai cây nhị phân để xác định xem chúng có giống hệt (identical) nhau hay không.

Bài toán: Bạn được cung cấp gốc của hai cây nhị phân và phải xác định xem những cây này có giống hệt nhau hay không. Các cây giống hệt nhau có cùng bố cục (layout) và dữ liệu tại mỗi node. Lưu ý: Những cây có cùng dữ liệu không nhất thiết phải giống hệt nhau. Điều quan trọng là cấu trúc của chúng.

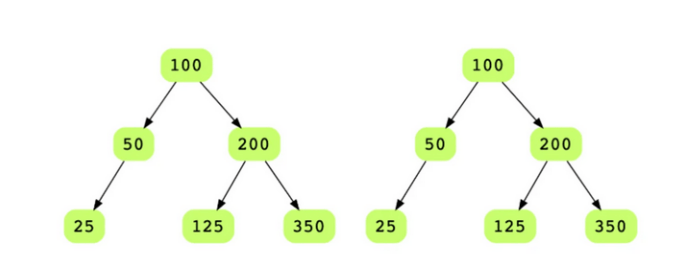
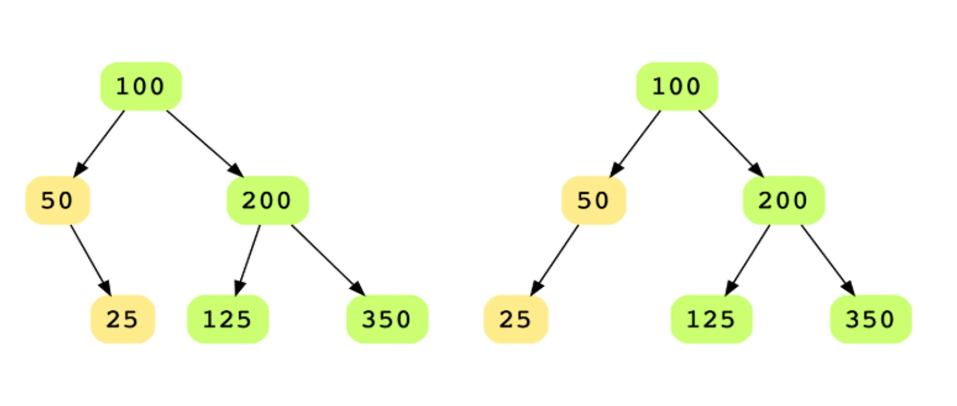
Hướng dẫn trả lời:

Vấn đề này có thể được giải quyết bằng cách đệ quy. Base case của đệ quy cho giải pháp này là nếu hai node được so sánh là null hoặc một trong số chúng là null.

Hai cây A và B giống hệt nhau nếu:

• Dữ liệu về gốc của chúng giống nhau hoặc cả hai gốc đều rỗng
• Cây con bên trái của A trùng với cây con bên trái của B
• Cây con bên phải của A trùng với cây con bên phải của B

Sử dụng duyệt theo chiều sâu trên cả hai cây và tiếp tục so sánh dữ liệu ở mỗi cấp để giải quyết vấn đề này.

Xem toàn bộ về giải pháp tại đây, và tại đây

Độ phức tạp:

• Độ phức tạp thời gian chạy: Tuyến tính, O (n)
• Độ phức tạp của bộ nhớ: O (h)trong trường hợp tốt nhất, hoặc nó sẽ là O (logn) cho cây cân bằng và trong trường hợp xấu nhất có thể là O (n ).

Q7: Mirror binary tree nodes

Mục tiêu của bài tập này là sử dụng thuật toán duyệt theo chiều sâu (depth first traversal) và phản chiếu từ dưới lên để phản chiếu các node của cây nhị phân.

Bài toán: Bạn được cung cấp node gốc của cây nhị phân và phải hoán đổi node con bên leftvà bên right cho mỗi node.

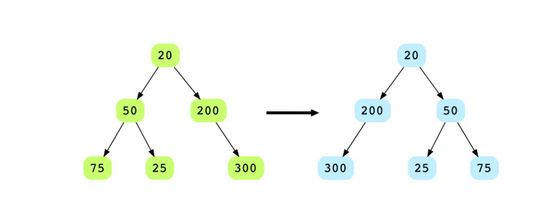
Hướng dẫn trả lời:

Chúng ta thực hiện duyệt theo thứ tự sau (post order traversal) của cây nhị phân. Đối với mọi node, hoán đổi node con bên trái của nó với node con bên phải. Chúng ta sử dụng DFS trên cây, để trước khi quay trở lại từ một node, tất cả các node con của nó đã được truy cập (và được sao chép)

Độ phức tạp:

• Độ phức tạp thời gian chạy: Tuyến tính, O (n)
• Độ phức tạp của bộ nhớ: Tuyến tính, O (n) trong trường hợp xấu nhất

Các câu hỏi phỏng vấn về String

Q8: Find all palindrome substrings

Mục tiêu của bài tập này là tìm các chuỗi con palindrome của một chuỗi đã cho.

Bài toán: Cho một chuỗi, hãy tìm tất cả các chuỗi con có nhiều hơn một ký tự là palindromes.

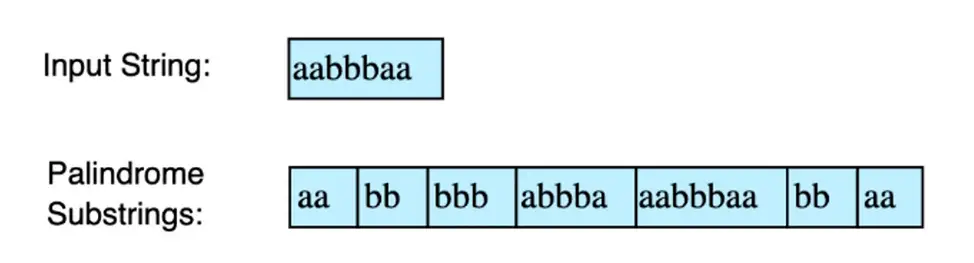
Hướng dẫn trả lời:

Đối với mỗi chữ cái trong chuỗi đầu vào, hãy bắt đầu mở rộng sang trái và phải trong khi kiểm tra độ dài chẵn và lẻ. Chuyển sang chữ cái tiếp theo nếu chúng ta biết palindrome không tồn tại ở đó.

Chúng ta mở rộng một ký tự sang trái và phải và so sánh. Nếu cả hai bằng nhau, chúng tôi in ra chuỗi con palindrome.

Xem thêm về giải pháp tại đây. Bạn cũng có thể xem thêm giải pháp viết bằng Java tại đây, bao gồm cả chuỗi con có 1 ký tự.

Độ phức tạp:

• Độ phức tạp thời gian chạy: Đa thức, O(n²)
• Độ phức tạp của bộ nhớ: Hằng số, O(1)

Q9: Reverse words in a sentence

Mục tiêu của bài tập này là đảo ngược các từ trong một chuỗi nhất định. Lưu ý các từ (word) được phân tách bằng khoảng trắng.

Bài toán: Đảo ngược thứ tự của các từ trong một câu đã cho (một mảng các ký tự). Lấy ví dụ những từ được đưa ra là “Hello World!”.

Hướng dẫn trả lời:

Có hai bước cần thực hiện. Đầu tiên, đảo ngược chuỗi. Sau đó, lướt qua chuỗi và đảo ngược từng từ.

Xem toàn bộ giải pháp tại đây

Độ phức tạp:

• Độ phức tạp thời gian chạy: Tuyến tính, O(n)
• Độ phức tạp của bộ nhớ: Hằng số, O(1)

Các câu hỏi phỏng về Dynamic programming

Q10: Largest Sum Subarray

Mục tiêu của bài tập này là sử dụng kỹ năng lập trình động và thuật toán Kadane để tìm mảng con có tổng lớn nhất.

Bài toán: Tìm mảng con có tổng lớn nhất. Trong mảng bên dưới, mảng con có tổng lớn nhất bắt đầu ở chỉ số 3 và kết thúc ở chỉ số 6 và với tổng lớn nhất là 12.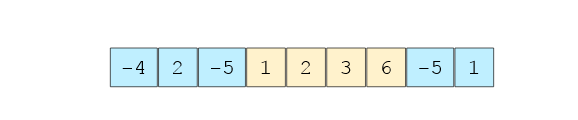

Hướng dẫn trả lời:

Chúng tôi sử dụng thuật toán của Kadane để giải quyết vấn đề này. Ý tưởng cơ bản của thuật toán này là quét toàn bộ mảng và tại mỗi vị trí tìm tổng lớn nhất của mảng con kết thúc ở đó. Điều này đạt được bằng cách giữ current_max cho chỉ số mảng hiện tại và global_max. Giải thuật như sau:

current_max = A[0]
global_max = A[0]
for i = 1 -> size of A
    if current_max is less than 0
        then current_max = A[i]
    otherwise 
        current_max = current_max + A[i]
    if global_max is less than current_max 
        then global_max = current_max

Độ phức tạp:

• Độ phức tạp thời gian chạy: Tuyến tính, O(n)
• Độ phức tạp của bộ nhớ: Hằng số, O(1)

Các câu hỏi phỏng vấn về toán học và thống kê

Q11: Power of a number

Mục tiêu của bài tập này là sử dụng giải thuật chia để trị (divide and conquer) và viết một hàm tính toán lũy thừa của một số.

Bài toán: Bạn được cho một cặp số, x và một số nguyên n, hãy viết một hàm tính x nâng lên lũy thừa n.

$power(2,5)=32$

power(3,4)=81

power(1.5,3)=3.375

power(2,−2)=0.25

Hướng dẫn trả lới:

Chúng ta có thể sử dụng giải thuật chia để trị để giải quyết vấn đề này một cách hiệu quả nhất. Trong bước chia, chúng ta tiếp tục chia n cho 2 một cách đệ quy cho đến khi đạt được trường hợp cơ sở (base case).

Trong bước kết hợp, chúng ta nhận được kết quả r của bài toán con và tính kết quả của bài toán hiện tại bằng cách sử dụng hai quy tắc dưới đây:

• Nếu n chẵn, kết quả là r * r (trong đó r là kết quả của bài toán con)
• Nếu n lẻ, kết quả là x * r * r (trong đó r là kết quả của bài toán con)

Độ phức tạp:

• Độ phức tạp thời gian chạy: Logarit, O (logn)
• Độ phức tạp của bộ nhớ: Logarit, O (logn)

Q12: Find all sum combinations

Mục tiêu của bài tập này là sử dụng thuật toán quay lui (Backtracking)  để tìm tất cả các tổ hợp tổng (sum combinations).

Bài toán: Cho một số nguyên dương, target, in ra tất cả các kết hợp có thể có của các số nguyên dương để có thể tạo ra  target. Đầu ra sẽ ở dạng một danh sách của các danh sách hoặc một mảng của mảng, vì mỗi phần tử trong danh sách sẽ là một danh sách khác chứa một tổ hợp tổng có thể có. Ví dụ: nếu bạn được cung cấp đầu vào 5, đây là các kết hợp tổng có thể có:

1, 4
2, 3
1, 1, 3
1, 2, 2
1, 1, 1, 2
1, 1, 1, 1, 1

Hướng dẫn trả lời:

• Sử dụng đệ quy
• Dùng hai mảng

Chúng ta duyệt đệ quy tất cả các kết hợp tổng có thể có và khi tổng bằng với mục tiêu, hãy in kết hợp đó. Thuật toán sẽ kiểm tra một cách đệ quy tất cả các số có thể có tổng bằng target.

Trong mỗi cuộc gọi đệ quy, có một vòng lặp for chạy từ đầu đến đích, ban đầu bắt đầu là 1. current_sum là biến được tăng lên với mỗi lần gọi đệ quy.

Mỗi khi một giá trị được thêm vào current_sum, nó cũng được thêm vào danh sách kết quả (result). Bất cứ khi nào current_sum bằng target, chúng ta biết rằng danh sách kết quả chứa một kết hợp có thể có cho target và danh sách này sau đó được nối vào danh sách đầu ra (output) cuối cùng.

Base condition of recursion:
 
if current_sum equals target
  print the output contents

Trước mỗi cuộc gọi đệ quy, một phần tử được thêm vào result. Tuy nhiên, sau mỗi lần gọi, phần tử này cũng bị xóa khỏi danh sách để thiết lập lại danh sách.

Xem thệm:

• Toàn bộ giải pháp và code mẫu
• Bài toán tương tự

Độ phức tạp:

• Độ phức tạp thời gian chạy: Hàm mũ, O(2ⁿ)
• Độ phức tạp của bộ nhớ: Tuyến tính, O(n)

Các câu hỏi về tìm kiếm và thiết kế

Q13: Search in rotated array

Mục tiêu của bài tập này là tìm kiếm một số nhất định cho trước trong một mảng đã được xoay (rotated array) theo một số nhất định và mảng đã được sắp xếp (trước khi xoay). Cố gắng giải quyết vấn đề bằng cách sử dụng tìm kiếm nhị phân.

Bài toán: Tìm kiếm một số nhất định trong một mảng đã sắp xếp, với các phần tử duy nhất, đã được xoay bởi một số tùy ý, giả sử rằng mảng không chứa các phần tử trùng lặp. Trả về -1 nếu số không tồn tại.

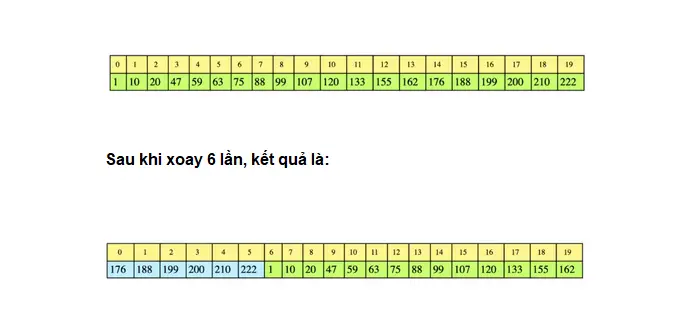
Hướng dẫn trả lời:

Giải pháp giống như một tìm kiếm nhị phân với một số sửa đổi. Lưu ý rằng ít nhất một nửa của mảng luôn được sắp xếp. Nếu số n nằm trong nửa đã sắp xếp của mảng, thì vấn đề của chúng ta là một tìm kiếm nhị phân cơ bản. Nếu không, hãy loại bỏ một nửa đã sắp xếp và kiểm tra một nửa chưa được sắp xếp.

Xem toàn bộ cách giải và code mẫu

Độ phức tạp:

Độ phức tạp thời gian chạy: Logarit, O(logn)

Độ phức tạp của bộ nhớ: Logarit, O(logn)

Q14: Implement a LRU cache

Mục tiêu của bài tập thiết kế này là thực hiện giải thuật Least Recently Used (LRU), một chiến lược bộ nhớ đệm phổ biến, sử dụng một danh sách được liên kết đôi (doubly linked list) và băm (hashing).

Bài toán: Thuật toán Least Recently Used (LRU) loại bỏ các phần tử khỏi bộ đệm để nhường chỗ cho các phần tử mới khi bộ đệm đầy, có nghĩa là nó sẽ loại bỏ các item ít được sử dụng gần đây nhất trước tiên.

Lấy ví dụ về bộ nhớ đệm có dung lượng 4 phần tử. Chúng ta lưu vào bộ nhớ cache các phần tử 1, 2, 3 và 4. Biểu đồ dưới đây đại diện cho trạng thái bộ nhớ cache sau lần truy cập đầu tiên của cả bốn phần tử.

Bây giờ chúng ta cần lưu vào bộ nhớ cache một phần tử 5 khác:

Hãy xem điều gì sẽ xảy ra khi 2 được truy cập lại. Bây giờ 3 trở thành dòng tiếp theo bị loại bỏ khỏi bộ nhớ cache:

Hướng dẫn trả lời:

Bộ nhớ đệm là một kỹ thuật để lưu trữ dữ liệu trong một bộ nhớ nhanh hơn (thường là RAM) để phục vụ các yêu cầu trong tương lai nhanh hơn. Các kho lưu trữ bộ nhớ đệm thường không đủ lớn để lưu trữ một tập dữ liệu đầy đủ. Chúng ta cần xóa dữ liệu khỏi bộ nhớ cache khi nó bị đầy.

LRU rất đơn giản và là một thuật toán thường được sử dụng cho quá trình này. Chúng ta loại bỏ dữ liệu cũ nhất khỏi bộ nhớ cache để chứa dữ liệu mới.

Để triển khai bộ đệm LRU, chúng ta sử dụng hai cấu trúc dữ liệu: một hashmap và một danh sách liên kết đôi. Một danh sách liên kết đôi giúp duy trì thứ tự loại bỏ và một hashmap giúp tra cứu O (1) các khóa được lưu trong bộ nhớ cache. Đây là thuật toán:

If the element exists in hashmap
    move the accessed element to the tail of the linked list
Otherwise,
    if eviction is needed i.e. cache is already full
        Remove the head element from doubly linked list and delete its hashmap entry
    Add the new element at the tail of linked list and in hashmap
Get from Cache and Return

Tham khảo thêm lời giải với Java code cho câu hỏi phỏng vấn lập trình này của Apple tại đây

Độ phức tạp:

Độ phức tạp thời gian chạy:

• get (hashset): Hằng số, O(1)
• set (hashset): Hằng số, O(1)
• Xóa đầu khi thêm một phần tử mới: Constant, O(1)
• Tìm kiếm để xóa và thêm vào đuôi: Linear, O(n)

Độ phức tạp của bộ nhớ: Tuyến tính, O(n), trong đó n là kích thước của bộ nhớ cache

Bài tham khảo: 30 câu hỏi phỏng vấn về lập trình của Apple trên educative.io